Note
Click here to download the full example code
Alleviating barren plateaus with local cost functions¶
Author: Thomas Storwick — Posted: 09 September 2020. Last updated: 28 January 2021.
Barren Plateaus¶
Barren plateaus are large regions of the cost function’s parameter space where the variance of the gradient is almost 0; or, put another way, the cost function landscape is flat. This means that a variational circuit initialized in one of these areas will be untrainable using any gradient-based algorithm.
In “Cost-Function-Dependent Barren Plateaus in Shallow Quantum Neural Networks” 1, Cerezo et al. demonstrate the idea that the barren plateau phenomenon can, under some circumstances, be avoided by using cost functions that only have information from part of the circuit. These local cost functions can be more robust against noise, and may have better-behaved gradients with no plateaus for shallow circuits.
Many variational quantum algorithms are constructed to use global cost functions. Information from the entire measurement is used to analyze the result of the circuit, and a cost function is calculated from this to quantify the circuit’s performance. A local cost function only considers information from a few qubits, and attempts to analyze the behavior of the entire circuit from this limited scope.
Cerezo et al. also handily prove that these local cost functions are bounded by the global ones, i.e., if a global cost function is formulated in the manner described by Cerezo et al., then the value of its corresponding local cost function will always be less than or equal to the value of the global cost function.
In this notebook, we investigate the effect of barren plateaus in variational quantum algorithms, and how they can be mitigated using local cost functions.
We first need to import the following modules.
import pennylane as qml
from pennylane import numpy as np
import matplotlib.pyplot as plt
from matplotlib.ticker import LinearLocator, FormatStrFormatter
np.random.seed(42)
Visualizing the problem¶
To start, let’s look at the task of learning the identity gate across multiple qubits. This will help us visualize the problem and get a sense of what is happening in the cost landscape.
First we define a number of wires we want to train on. The work by Cerezo et al. shows that circuits are trainable under certain regimes, so how many qubits we train on will effect our results.
wires = 6
dev = qml.device("default.qubit", wires=wires, shots=10000)
Next, we want to define our QNodes and our circuit ansatz. For this simple example, an ansatz that works well is simply a rotation along X, and a rotation along Y, repeated across all the qubits.
We will also define our cost functions here. Since we are trying to learn the identity gate, a natural cost function is 1 minus the probability of measuring the zero state, denoted here as \(1 - p_{|0\rangle}\).
We will apply this across all qubits for our global cost function, i.e.,
and for the local cost function, we will sum the individual contributions from each qubit:
It might be clear to some readers now why this function can perform better. By formatting our local cost function in this way, we have essentially divided the problem up into multiple single-qubit terms, and summed all the results up.
To implement this, we will define a separate QNode for the local cost function and the global cost function.
def global_cost_simple(rotations):
for i in range(wires):
qml.RX(rotations[0][i], wires=i)
qml.RY(rotations[1][i], wires=i)
return qml.probs(wires=range(wires))
def local_cost_simple(rotations):
for i in range(wires):
qml.RX(rotations[0][i], wires=i)
qml.RY(rotations[1][i], wires=i)
return [qml.probs(wires=i) for i in range(wires)]
global_circuit = qml.QNode(global_cost_simple, dev, interface="autograd")
local_circuit = qml.QNode(local_cost_simple, dev, interface="autograd")
def cost_local(rotations):
return 1 - np.sum([i for (i, _) in local_circuit(rotations)])/wires
def cost_global(rotations):
return 1 - global_circuit(rotations)[0]
To analyze each of the circuits, we provide some random initial parameters for each rotation.
RX = np.random.uniform(low=-np.pi, high=np.pi)
RY = np.random.uniform(low=-np.pi, high=np.pi)
rotations = [[RX for i in range(wires)], [RY for i in range(wires)]]
Examining the results:
print("Global Cost: {: .7f}".format(cost_global(rotations)))
print("Local Cost: {: .7f}".format(cost_local(rotations)))
qml.drawer.use_style('black_white')
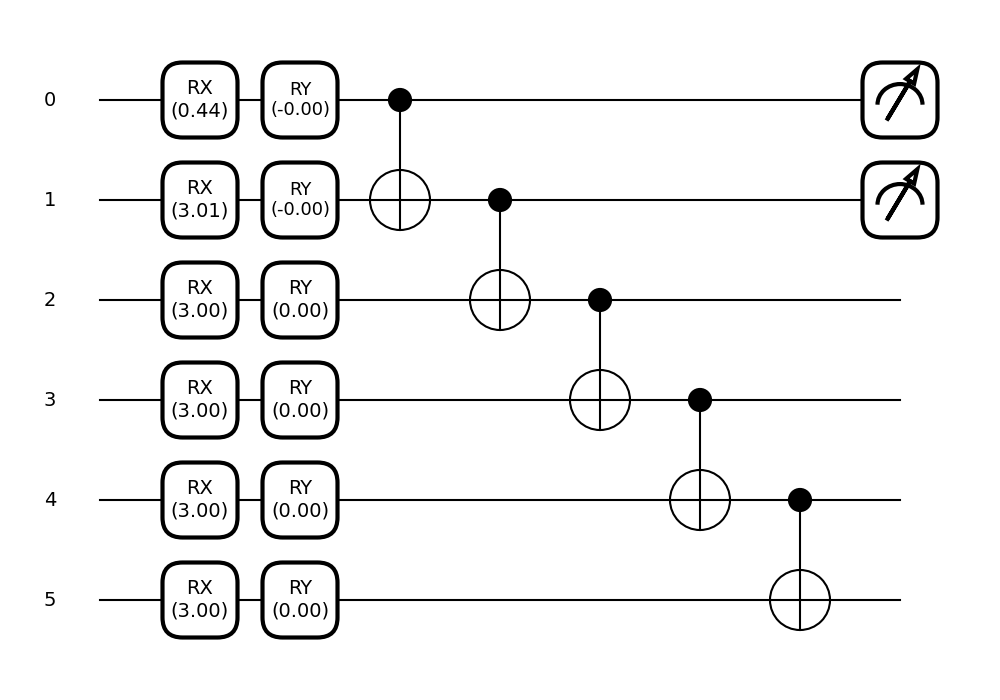
fig1, ax1 = qml.draw_mpl(global_circuit, decimals=2)(rotations)
fig1.suptitle("Global Cost", fontsize='xx-large')
plt.show()
fig2, ax2 = qml.draw_mpl(local_circuit, decimals=2)(rotations)
fig2.suptitle("Local Cost", fontsize='xx-large')
plt.show()
Out:
Global Cost: 0.9999000
Local Cost: 0.8373000
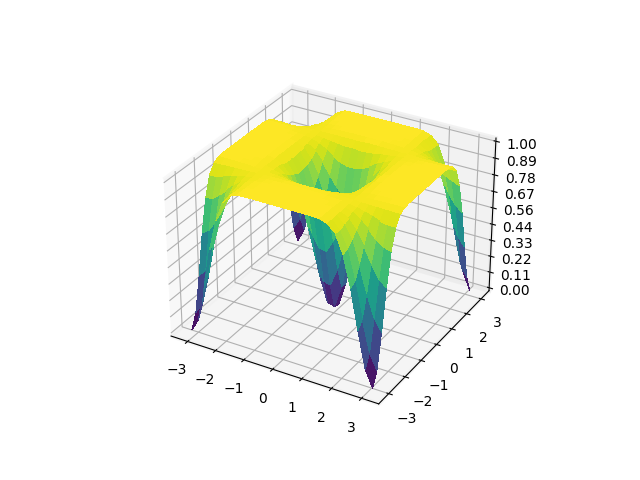
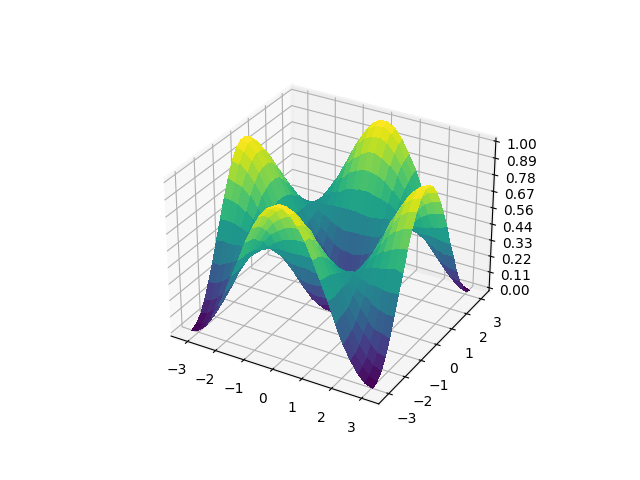
With this simple example, we can visualize the cost function, and see the barren plateau effect graphically. Although there are \(2n\) (where \(n\) is the number of qubits) parameters, in order to plot the cost landscape we must constrain ourselves. We will consider the case where all X rotations have the same value, and all the Y rotations have the same value.
Firstly, we look at the global cost function. When plotting the cost function across 6 qubits, much of the cost landscape is flat, and difficult to train (even with a circuit depth of only 2!). This effect will worsen as the number of qubits increases.
def generate_surface(cost_function):
Z = []
Z_assembler = []
X = np.arange(-np.pi, np.pi, 0.25)
Y = np.arange(-np.pi, np.pi, 0.25)
X, Y = np.meshgrid(X, Y)
for x in X[0, :]:
for y in Y[:, 0]:
rotations = [[x for i in range(wires)], [y for i in range(wires)]]
Z_assembler.append(cost_function(rotations))
Z.append(Z_assembler)
Z_assembler = []
Z = np.asarray(Z)
return Z
def plot_surface(surface):
X = np.arange(-np.pi, np.pi, 0.25)
Y = np.arange(-np.pi, np.pi, 0.25)
X, Y = np.meshgrid(X, Y)
fig = plt.figure()
ax = fig.add_subplot(111, projection="3d")
surf = ax.plot_surface(X, Y, surface, cmap="viridis", linewidth=0, antialiased=False)
ax.set_zlim(0, 1)
ax.zaxis.set_major_locator(LinearLocator(10))
ax.zaxis.set_major_formatter(FormatStrFormatter("%.02f"))
plt.show()
global_surface = generate_surface(cost_global)
plot_surface(global_surface)
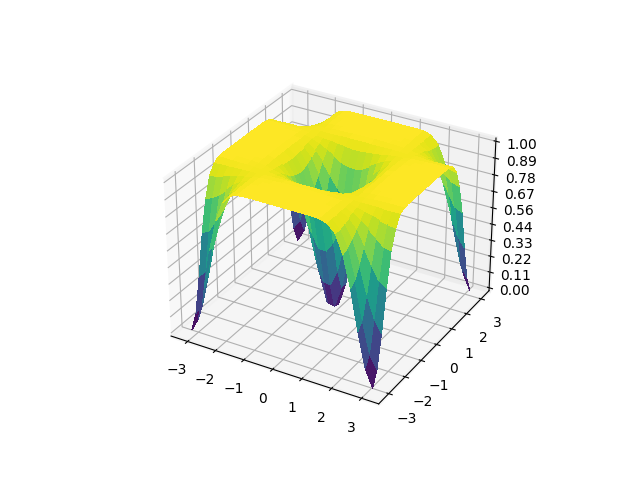
However, when we change to the local cost function, the cost landscape becomes much more trainable as the size of the barren plateau decreases.
local_surface = generate_surface(cost_local)
plot_surface(local_surface)
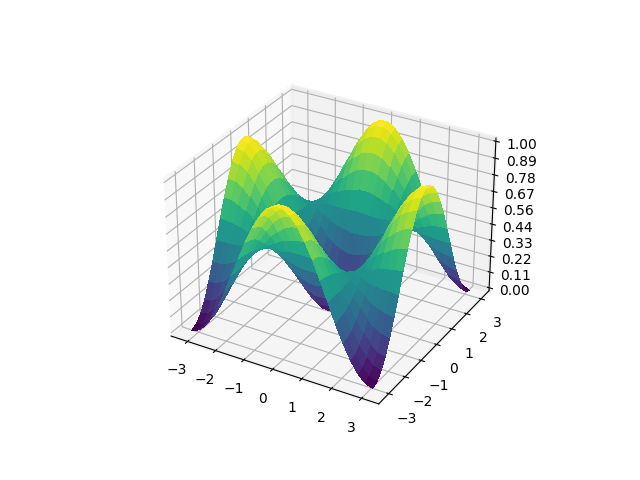
Those are some nice pictures, but how do they reflect actual trainability? Let us try training both the local and global cost functions. To simplify this model, let’s modify our cost function from
where we sum the marginal probabilities of each qubit, to
where we only consider the probability of a single qubit to be in the 0 state.
While we’re at it, let us make our ansatz a little more like one we would encounter while trying to solve a VQE problem, and add entanglement.
def global_cost_simple(rotations):
for i in range(wires):
qml.RX(rotations[0][i], wires=i)
qml.RY(rotations[1][i], wires=i)
qml.broadcast(qml.CNOT, wires=range(wires), pattern="chain")
return qml.probs(wires=range(wires))
def local_cost_simple(rotations):
for i in range(wires):
qml.RX(rotations[0][i], wires=i)
qml.RY(rotations[1][i], wires=i)
qml.broadcast(qml.CNOT, wires=range(wires), pattern="chain")
return qml.probs(wires=[0])
global_circuit = qml.QNode(global_cost_simple, dev, interface="autograd")
local_circuit = qml.QNode(local_cost_simple, dev, interface="autograd")
def cost_local(rotations):
return 1 - local_circuit(rotations)[0]
def cost_global(rotations):
return 1 - global_circuit(rotations)[0]
Of course, now that we’ve changed both our cost function and our circuit, we will need to scan the cost landscape again.
global_surface = generate_surface(cost_global)
plot_surface(global_surface)
local_surface = generate_surface(cost_local)
plot_surface(local_surface)
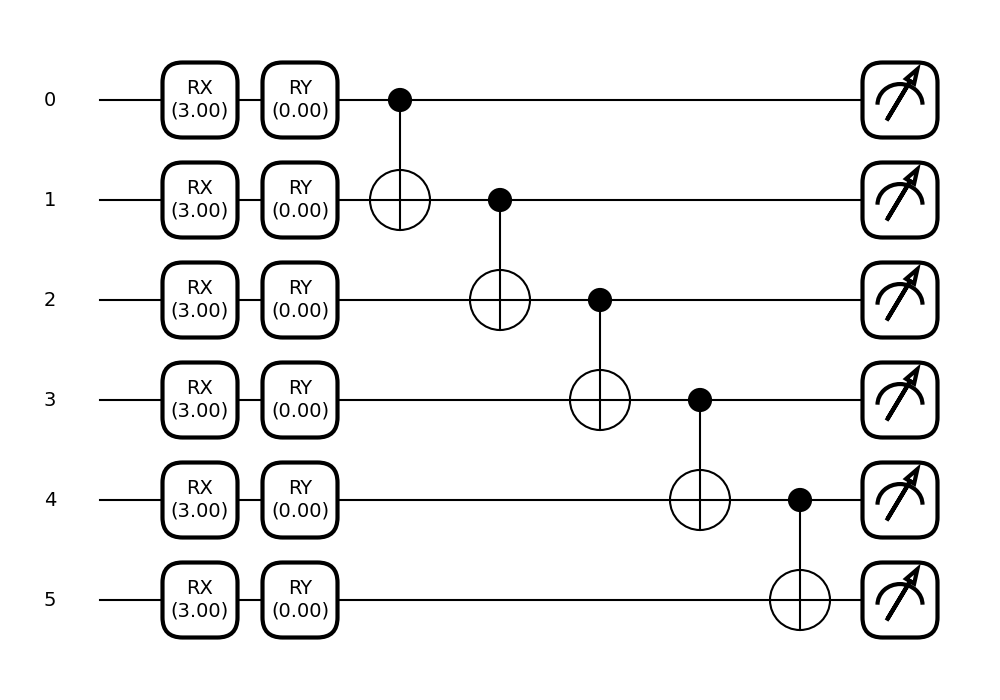
It seems our changes didn’t significantly alter the overall cost landscape. This probably isn’t a general trend, but it is a nice surprise. Now, let us get back to training the local and global cost functions. Because we have a visualization of the total cost landscape, let’s pick a point to exaggerate the problem. One of the worst points in the landscape is \((\pi,0)\) as it is in the middle of the plateau, so let’s use that.
rotations = np.array([[3.] * len(range(wires)), [0.] * len(range(wires))], requires_grad=True)
opt = qml.GradientDescentOptimizer(stepsize=0.2)
steps = 100
params_global = rotations
for i in range(steps):
# update the circuit parameters
params_global = opt.step(cost_global, params_global)
if (i + 1) % 5 == 0:
print("Cost after step {:5d}: {: .7f}".format(i + 1, cost_global(params_global)))
if cost_global(params_global) < 0.1:
break
fig, ax = qml.draw_mpl(global_circuit, decimals=2)(params_global)
plt.show()
Out:
Cost after step 5: 1.0000000
Cost after step 10: 1.0000000
Cost after step 15: 1.0000000
Cost after step 20: 1.0000000
Cost after step 25: 1.0000000
Cost after step 30: 1.0000000
Cost after step 35: 1.0000000
Cost after step 40: 1.0000000
Cost after step 45: 1.0000000
Cost after step 50: 1.0000000
Cost after step 55: 1.0000000
Cost after step 60: 1.0000000
Cost after step 65: 1.0000000
Cost after step 70: 1.0000000
Cost after step 75: 1.0000000
Cost after step 80: 1.0000000
Cost after step 85: 1.0000000
Cost after step 90: 1.0000000
Cost after step 95: 1.0000000
Cost after step 100: 1.0000000
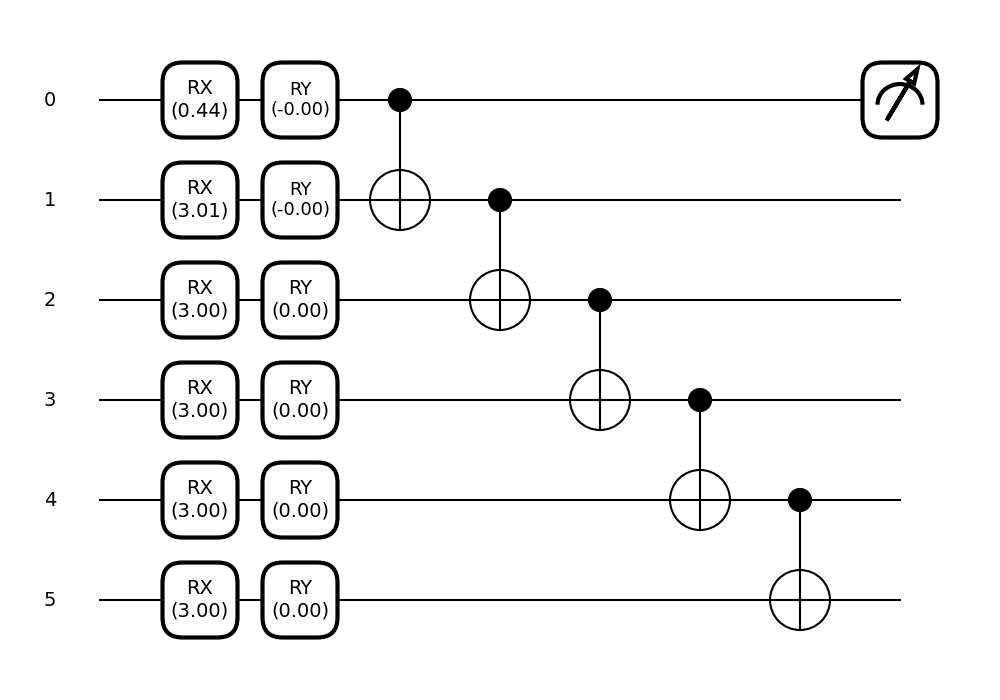
After 100 steps, the cost function is still exactly 1. Clearly we are in an “untrainable” area. Now, let us limit ourselves to the local cost function and see how it performs.
rotations = np.array([[3. for i in range(wires)], [0. for i in range(wires)]], requires_grad=True)
opt = qml.GradientDescentOptimizer(stepsize=0.2)
steps = 100
params_local = rotations
for i in range(steps):
# update the circuit parameters
params_local = opt.step(cost_local, params_local)
if (i + 1) % 5 == 0:
print("Cost after step {:5d}: {: .7f}".format(i + 1, cost_local(params_local)))
if cost_local(params_local) < 0.05:
break
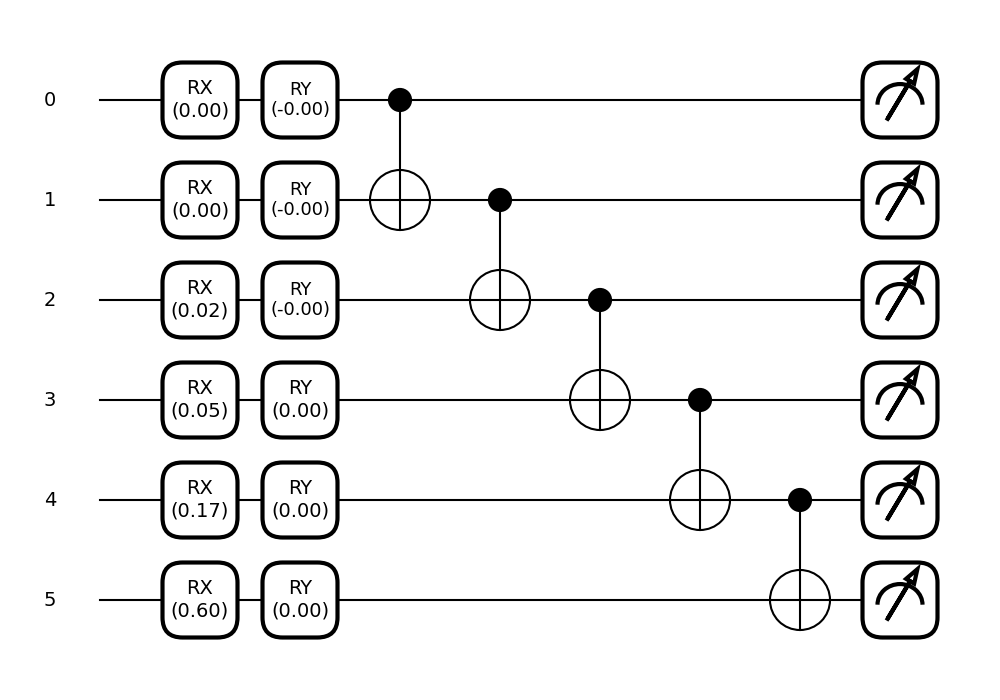
fig, ax = qml.draw_mpl(local_circuit, decimals=2)(params_local)
plt.show()
Out:
Cost after step 5: 0.9871000
Cost after step 10: 0.9651000
Cost after step 15: 0.9173000
Cost after step 20: 0.8059000
Cost after step 25: 0.6213000
Cost after step 30: 0.3703000
Cost after step 35: 0.1821000
Cost after step 40: 0.0684000
It trained! And much faster than the global case. However, we know our local cost function is bounded by the global one, but just how much have we trained it?
cost_global(params_local)
Out:
1.0
Interestingly, the global cost function is still 1. If we trained the local cost function, why hasn’t the global cost function changed?
The answer is that we have trained the global cost a little bit, but
not enough to see a change with only 10000 shots. To see the effect,
we’ll need to increase the number of shots to an unreasonable amount.
Instead, making the backend analytic by setting shots to None, gives
us the exact representation.
dev.shots = None
global_circuit = qml.QNode(global_cost_simple, dev, interface="autograd")
print(
"Current cost: "
+ str(cost_global(params_local))
+ ".\nInitial cost: "
+ str(cost_global([[3.0 for i in range(wires)], [0 for i in range(wires)]]))
+ ".\nDifference: "
+ str(
cost_global([[3.0 for i in range(wires)], [0 for i in range(wires)]])
- cost_global(params_local)
)
)
Out:
Current cost: 0.9999999999972213.
Initial cost: 0.9999999999999843.
Difference: 2.763012041384627e-12
Our circuit has definitely been trained, but not a useful amount. If we attempt to use this circuit, it would act the same as if we never trained at all. Furthermore, if we now attempt to train the global cost function, we are still firmly in the plateau region. In order to fully train the global circuit, we will need to increase the locality gradually as we train.
def tunable_cost_simple(rotations):
for i in range(wires):
qml.RX(rotations[0][i], wires=i)
qml.RY(rotations[1][i], wires=i)
qml.broadcast(qml.CNOT, wires=range(wires), pattern="chain")
return qml.probs(range(locality))
def cost_tunable(rotations):
return 1 - tunable_circuit(rotations)[0]
dev.shots = 10000
tunable_circuit = qml.QNode(tunable_cost_simple, dev, interface="autograd")
locality = 2
params_tunable = params_local
fig, ax = qml.draw_mpl(tunable_circuit, decimals=2)(params_tunable)
plt.show()
print(cost_tunable(params_tunable))
locality = 2
opt = qml.GradientDescentOptimizer(stepsize=0.1)
steps = 600
for i in range(steps):
# update the circuit parameters
params_tunable = opt.step(cost_tunable, params_tunable)
runCost = cost_tunable(params_tunable)
if (i + 1) % 10 == 0:
print(
"Cost after step {:5d}: {: .7f}".format(i + 1, runCost)
+ ". Locality: "
+ str(locality)
)
if runCost < 0.1 and locality < wires:
print("---Switching Locality---")
locality += 1
continue
elif runCost < 0.1 and locality >= wires:
break
fig, ax = qml.draw_mpl(tunable_circuit, decimals=2)(params_tunable)
plt.show()
Out:
0.9957
Cost after step 10: 0.9909000. Locality: 2
Cost after step 20: 0.9753000. Locality: 2
Cost after step 30: 0.9275000. Locality: 2
Cost after step 40: 0.8386000. Locality: 2
Cost after step 50: 0.6821000. Locality: 2
Cost after step 60: 0.4353000. Locality: 2
Cost after step 70: 0.2264000. Locality: 2
Cost after step 80: 0.0923000. Locality: 2
---Switching Locality---
Cost after step 90: 0.9901000. Locality: 3
Cost after step 100: 0.9737000. Locality: 3
Cost after step 110: 0.9400000. Locality: 3
Cost after step 120: 0.8711000. Locality: 3
Cost after step 130: 0.7228000. Locality: 3
Cost after step 140: 0.5156000. Locality: 3
Cost after step 150: 0.2846000. Locality: 3
Cost after step 160: 0.1285000. Locality: 3
---Switching Locality---
Cost after step 170: 0.9899000. Locality: 4
Cost after step 180: 0.9799000. Locality: 4
Cost after step 190: 0.9512000. Locality: 4
Cost after step 200: 0.8964000. Locality: 4
Cost after step 210: 0.7683000. Locality: 4
Cost after step 220: 0.5752000. Locality: 4
Cost after step 230: 0.3314000. Locality: 4
Cost after step 240: 0.1575000. Locality: 4
---Switching Locality---
Cost after step 250: 0.9942000. Locality: 5
Cost after step 260: 0.9866000. Locality: 5
Cost after step 270: 0.9641000. Locality: 5
Cost after step 280: 0.9120000. Locality: 5
Cost after step 290: 0.8136000. Locality: 5
Cost after step 300: 0.6380000. Locality: 5
Cost after step 310: 0.4004000. Locality: 5
Cost after step 320: 0.1996000. Locality: 5
---Switching Locality---
Cost after step 330: 0.9945000. Locality: 6
Cost after step 340: 0.9873000. Locality: 6
Cost after step 350: 0.9689000. Locality: 6
Cost after step 360: 0.9288000. Locality: 6
Cost after step 370: 0.8476000. Locality: 6
Cost after step 380: 0.6711000. Locality: 6
Cost after step 390: 0.4527000. Locality: 6
Cost after step 400: 0.2342000. Locality: 6
Cost after step 410: 0.1014000. Locality: 6
A more thorough analysis¶
Now the circuit can be trained, even though we started from a place where the global function has a barren plateau. The significance of this is that we can now train from every starting location in this example.
But, how often does this problem occur? If we wanted to train this circuit from a random starting point, how often would we be stuck in a plateau? To investigate this, let’s attempt to train the global cost function using random starting positions and count how many times we run into a barren plateau.
Let’s use a number of qubits we are more likely to use in a real variational circuit: n=10. We will say that after 400 steps, any run with a cost function of less than 0.9 (chosen arbitrarily) will probably be trainable given more time. Any run with a greater cost function will probably be in a plateau.
This may take up to 15 minutes.
samples = 10
plateau = 0
trained = 0
opt = qml.GradientDescentOptimizer(stepsize=0.2)
steps = 400
wires = 8
dev = qml.device("default.qubit", wires=wires, shots=10000)
global_circuit = qml.QNode(global_cost_simple, dev, interface="autograd")
for runs in range(samples):
print("--- New run! ---")
has_been_trained = False
params_global = np.random.uniform(-np.pi, np.pi, (2, wires), requires_grad=True)
for i in range(steps):
# update the circuit parameters
params_global = opt.step(cost_global, params_global)
if (i + 1) % 20 == 0:
print("Cost after step {:5d}: {: .7f}".format(i + 1, cost_global(params_global)))
if cost_global(params_global) < 0.9:
has_been_trained = True
break
if has_been_trained:
trained = trained + 1
else:
plateau = plateau + 1
print("Trained: {:5d}".format(trained))
print("Plateau'd: {:5d}".format(plateau))
samples = 10
plateau = 0
trained = 0
opt = qml.GradientDescentOptimizer(stepsize=0.2)
steps = 400
wires = 8
dev = qml.device("default.qubit", wires=wires, shots=10000)
tunable_circuit = qml.QNode(tunable_cost_simple, dev, interface="autograd")
for runs in range(samples):
locality = 1
print("--- New run! ---")
has_been_trained = False
params_tunable = np.random.uniform(-np.pi, np.pi, (2, wires), requires_grad=True)
for i in range(steps):
# update the circuit parameters
params_tunable = opt.step(cost_tunable, params_tunable)
runCost = cost_tunable(params_tunable)
if (i + 1) % 10 == 0:
print(
"Cost after step {:5d}: {: .7f}".format(i + 1, runCost)
+ ". Locality: "
+ str(locality)
)
if runCost < 0.5 and locality < wires:
print("---Switching Locality---")
locality += 1
continue
elif runCost < 0.1 and locality >= wires:
trained = trained + 1
has_been_trained = True
break
if not has_been_trained:
plateau = plateau + 1
print("Trained: {:5d}".format(trained))
print("Plateau'd: {:5d}".format(plateau))
Out:
--- New run! ---
Cost after step 20: 1.0000000
Cost after step 40: 1.0000000
Cost after step 60: 1.0000000
Cost after step 80: 1.0000000
Cost after step 100: 1.0000000
Cost after step 120: 1.0000000
Cost after step 140: 1.0000000
Cost after step 160: 1.0000000
Cost after step 180: 1.0000000
Cost after step 200: 1.0000000
Cost after step 220: 1.0000000
Cost after step 240: 1.0000000
Cost after step 260: 1.0000000
Cost after step 280: 1.0000000
Cost after step 300: 1.0000000
Cost after step 320: 1.0000000
Cost after step 340: 1.0000000
Cost after step 360: 1.0000000
Cost after step 380: 1.0000000
Cost after step 400: 1.0000000
Trained: 0
Plateau'd: 1
--- New run! ---
Cost after step 20: 0.9993000
Cost after step 40: 0.9994000
Cost after step 60: 0.9995000
Cost after step 80: 0.9994000
Cost after step 100: 0.9996000
Cost after step 120: 0.9995000
Cost after step 140: 0.9986000
Cost after step 160: 0.9993000
Cost after step 180: 0.9991000
Cost after step 200: 0.9996000
Cost after step 220: 0.9985000
Cost after step 240: 0.9989000
Cost after step 260: 0.9993000
Cost after step 280: 0.9991000
Cost after step 300: 0.9990000
Cost after step 320: 0.9987000
Cost after step 340: 0.9987000
Cost after step 360: 0.9994000
Cost after step 380: 0.9985000
Cost after step 400: 0.9991000
Trained: 0
Plateau'd: 2
--- New run! ---
Cost after step 20: 0.9976000
Cost after step 40: 0.9967000
Cost after step 60: 0.9970000
Cost after step 80: 0.9964000
Cost after step 100: 0.9956000
Cost after step 120: 0.9965000
Cost after step 140: 0.9958000
Cost after step 160: 0.9931000
Cost after step 180: 0.9940000
Cost after step 200: 0.9908000
Cost after step 220: 0.9887000
Cost after step 240: 0.9834000
Cost after step 260: 0.9821000
Cost after step 280: 0.9742000
Cost after step 300: 0.9576000
Cost after step 320: 0.9330000
Trained: 1
Plateau'd: 2
--- New run! ---
Cost after step 20: 0.9998000
Cost after step 40: 0.9997000
Cost after step 60: 0.9996000
Cost after step 80: 0.9994000
Cost after step 100: 0.9994000
Cost after step 120: 0.9996000
Cost after step 140: 0.9997000
Cost after step 160: 0.9992000
Cost after step 180: 0.9991000
Cost after step 200: 0.9992000
Cost after step 220: 0.9990000
Cost after step 240: 0.9986000
Cost after step 260: 0.9989000
Cost after step 280: 0.9988000
Cost after step 300: 0.9972000
Cost after step 320: 0.9982000
Cost after step 340: 0.9981000
Cost after step 360: 0.9979000
Cost after step 380: 0.9977000
Cost after step 400: 0.9972000
Trained: 1
Plateau'd: 3
--- New run! ---
Cost after step 20: 1.0000000
Cost after step 40: 1.0000000
Cost after step 60: 0.9999000
Cost after step 80: 1.0000000
Cost after step 100: 1.0000000
Cost after step 120: 1.0000000
Cost after step 140: 1.0000000
Cost after step 160: 0.9999000
Cost after step 180: 1.0000000
Cost after step 200: 1.0000000
Cost after step 220: 1.0000000
Cost after step 240: 1.0000000
Cost after step 260: 1.0000000
Cost after step 280: 1.0000000
Cost after step 300: 1.0000000
Cost after step 320: 1.0000000
Cost after step 340: 1.0000000
Cost after step 360: 0.9998000
Cost after step 380: 1.0000000
Cost after step 400: 1.0000000
Trained: 1
Plateau'd: 4
--- New run! ---
Cost after step 20: 0.9950000
Cost after step 40: 0.9957000
Cost after step 60: 0.9931000
Cost after step 80: 0.9920000
Cost after step 100: 0.9925000
Cost after step 120: 0.9908000
Cost after step 140: 0.9865000
Cost after step 160: 0.9861000
Cost after step 180: 0.9846000
Cost after step 200: 0.9767000
Cost after step 220: 0.9696000
Cost after step 240: 0.9560000
Cost after step 260: 0.9276000
Trained: 2
Plateau'd: 4
--- New run! ---
Cost after step 20: 0.9989000
Cost after step 40: 0.9979000
Cost after step 60: 0.9979000
Cost after step 80: 0.9982000
Cost after step 100: 0.9984000
Cost after step 120: 0.9986000
Cost after step 140: 0.9978000
Cost after step 160: 0.9976000
Cost after step 180: 0.9967000
Cost after step 200: 0.9972000
Cost after step 220: 0.9958000
Cost after step 240: 0.9966000
Cost after step 260: 0.9966000
Cost after step 280: 0.9952000
Cost after step 300: 0.9958000
Cost after step 320: 0.9972000
Cost after step 340: 0.9953000
Cost after step 360: 0.9934000
Cost after step 380: 0.9929000
Cost after step 400: 0.9916000
Trained: 2
Plateau'd: 5
--- New run! ---
Cost after step 20: 0.9988000
Cost after step 40: 0.9980000
Cost after step 60: 0.9978000
Cost after step 80: 0.9986000
Cost after step 100: 0.9978000
Cost after step 120: 0.9977000
Cost after step 140: 0.9974000
Cost after step 160: 0.9976000
Cost after step 180: 0.9975000
Cost after step 200: 0.9970000
Cost after step 220: 0.9972000
Cost after step 240: 0.9961000
Cost after step 260: 0.9960000
Cost after step 280: 0.9953000
Cost after step 300: 0.9947000
Cost after step 320: 0.9945000
Cost after step 340: 0.9912000
Cost after step 360: 0.9916000
Cost after step 380: 0.9866000
Cost after step 400: 0.9822000
Trained: 2
Plateau'd: 6
--- New run! ---
Cost after step 20: 1.0000000
Cost after step 40: 1.0000000
Cost after step 60: 1.0000000
Cost after step 80: 1.0000000
Cost after step 100: 1.0000000
Cost after step 120: 1.0000000
Cost after step 140: 1.0000000
Cost after step 160: 1.0000000
Cost after step 180: 1.0000000
Cost after step 200: 1.0000000
Cost after step 220: 1.0000000
Cost after step 240: 1.0000000
Cost after step 260: 1.0000000
Cost after step 280: 1.0000000
Cost after step 300: 1.0000000
Cost after step 320: 1.0000000
Cost after step 340: 1.0000000
Cost after step 360: 1.0000000
Cost after step 380: 1.0000000
Cost after step 400: 1.0000000
Trained: 2
Plateau'd: 7
--- New run! ---
Cost after step 20: 1.0000000
Cost after step 40: 1.0000000
Cost after step 60: 1.0000000
Cost after step 80: 1.0000000
Cost after step 100: 0.9999000
Cost after step 120: 1.0000000
Cost after step 140: 1.0000000
Cost after step 160: 1.0000000
Cost after step 180: 1.0000000
Cost after step 200: 1.0000000
Cost after step 220: 1.0000000
Cost after step 240: 1.0000000
Cost after step 260: 1.0000000
Cost after step 280: 1.0000000
Cost after step 300: 1.0000000
Cost after step 320: 1.0000000
Cost after step 340: 1.0000000
Cost after step 360: 1.0000000
Cost after step 380: 1.0000000
Cost after step 400: 1.0000000
Trained: 2
Plateau'd: 8
--- New run! ---
---Switching Locality---
Cost after step 10: 0.6137000. Locality: 2
---Switching Locality---
Cost after step 20: 0.5159000. Locality: 3
---Switching Locality---
Cost after step 30: 0.7040000. Locality: 4
Cost after step 40: 0.5823000. Locality: 4
---Switching Locality---
Cost after step 50: 0.5055000. Locality: 5
---Switching Locality---
Cost after step 60: 0.6965000. Locality: 6
Cost after step 70: 0.5823000. Locality: 6
---Switching Locality---
Cost after step 80: 0.8792000. Locality: 7
Cost after step 90: 0.7172000. Locality: 7
---Switching Locality---
Cost after step 100: 0.9741000. Locality: 8
Cost after step 110: 0.9329000. Locality: 8
Cost after step 120: 0.8278000. Locality: 8
Cost after step 130: 0.5973000. Locality: 8
Cost after step 140: 0.2649000. Locality: 8
Trained: 1
Plateau'd: 0
--- New run! ---
---Switching Locality---
Cost after step 10: 0.6273000. Locality: 2
---Switching Locality---
---Switching Locality---
Cost after step 20: 0.9218000. Locality: 4
Cost after step 30: 0.8247000. Locality: 4
Cost after step 40: 0.5992000. Locality: 4
---Switching Locality---
Cost after step 50: 0.6852000. Locality: 5
Cost after step 60: 0.6003000. Locality: 5
Cost after step 70: 0.5220000. Locality: 5
---Switching Locality---
Cost after step 80: 0.5100000. Locality: 6
---Switching Locality---
---Switching Locality---
Cost after step 90: 0.4677000. Locality: 8
Cost after step 100: 0.1562000. Locality: 8
Trained: 2
Plateau'd: 0
--- New run! ---
---Switching Locality---
---Switching Locality---
---Switching Locality---
---Switching Locality---
Cost after step 10: 0.5405000. Locality: 5
---Switching Locality---
Cost after step 20: 0.6024000. Locality: 6
---Switching Locality---
Cost after step 30: 0.6060000. Locality: 7
---Switching Locality---
Cost after step 40: 0.5009000. Locality: 8
Cost after step 50: 0.1676000. Locality: 8
Trained: 3
Plateau'd: 0
--- New run! ---
Cost after step 10: 0.4871000. Locality: 1
---Switching Locality---
Cost after step 20: 0.4948000. Locality: 2
---Switching Locality---
Cost after step 30: 0.6627000. Locality: 3
---Switching Locality---
Cost after step 40: 0.5826000. Locality: 4
---Switching Locality---
Cost after step 50: 0.5234000. Locality: 5
---Switching Locality---
---Switching Locality---
Cost after step 60: 0.6394000. Locality: 7
---Switching Locality---
Cost after step 70: 0.3126000. Locality: 8
Trained: 4
Plateau'd: 0
--- New run! ---
Cost after step 10: 0.5485000. Locality: 1
---Switching Locality---
Cost after step 20: 0.6393000. Locality: 2
---Switching Locality---
Cost after step 30: 0.8061000. Locality: 3
Cost after step 40: 0.7073000. Locality: 3
Cost after step 50: 0.6144000. Locality: 3
Cost after step 60: 0.4888000. Locality: 3
---Switching Locality---
Cost after step 70: 0.6102000. Locality: 4
---Switching Locality---
Cost after step 80: 0.4909000. Locality: 5
---Switching Locality---
Cost after step 90: 0.7897000. Locality: 6
Cost after step 100: 0.4939000. Locality: 6
---Switching Locality---
Cost after step 110: 0.7063000. Locality: 7
Cost after step 120: 0.5323000. Locality: 7
---Switching Locality---
Cost after step 130: 0.2921000. Locality: 8
Trained: 5
Plateau'd: 0
--- New run! ---
---Switching Locality---
Cost after step 10: 0.7449000. Locality: 2
Cost after step 20: 0.5005000. Locality: 2
---Switching Locality---
---Switching Locality---
---Switching Locality---
Cost after step 30: 0.7292000. Locality: 5
Cost after step 40: 0.4696000. Locality: 5
---Switching Locality---
---Switching Locality---
Cost after step 50: 0.5099000. Locality: 7
---Switching Locality---
Cost after step 60: 0.6587000. Locality: 8
Cost after step 70: 0.4912000. Locality: 8
Cost after step 80: 0.2440000. Locality: 8
Trained: 6
Plateau'd: 0
--- New run! ---
---Switching Locality---
---Switching Locality---
Cost after step 10: 0.8510000. Locality: 3
Cost after step 20: 0.7255000. Locality: 3
Cost after step 30: 0.5811000. Locality: 3
---Switching Locality---
Cost after step 40: 0.6300000. Locality: 4
---Switching Locality---
Cost after step 50: 0.8801000. Locality: 5
Cost after step 60: 0.7395000. Locality: 5
---Switching Locality---
Cost after step 70: 0.8948000. Locality: 6
Cost after step 80: 0.7399000. Locality: 6
---Switching Locality---
Cost after step 90: 0.7139000. Locality: 7
Cost after step 100: 0.5959000. Locality: 7
---Switching Locality---
Cost after step 110: 0.5939000. Locality: 8
Cost after step 120: 0.2906000. Locality: 8
Trained: 7
Plateau'd: 0
--- New run! ---
---Switching Locality---
Cost after step 10: 0.6986000. Locality: 2
Cost after step 20: 0.6273000. Locality: 2
Cost after step 30: 0.5645000. Locality: 2
Cost after step 40: 0.5016000. Locality: 2
---Switching Locality---
Cost after step 50: 0.9048000. Locality: 3
Cost after step 60: 0.7903000. Locality: 3
Cost after step 70: 0.5948000. Locality: 3
---Switching Locality---
---Switching Locality---
Cost after step 80: 0.5600000. Locality: 5
---Switching Locality---
Cost after step 90: 0.8307000. Locality: 6
Cost after step 100: 0.6442000. Locality: 6
---Switching Locality---
Cost after step 110: 0.7075000. Locality: 7
Cost after step 120: 0.5936000. Locality: 7
---Switching Locality---
Cost after step 130: 0.7649000. Locality: 8
Cost after step 140: 0.6810000. Locality: 8
Cost after step 150: 0.5936000. Locality: 8
Cost after step 160: 0.4526000. Locality: 8
Cost after step 170: 0.1974000. Locality: 8
Trained: 8
Plateau'd: 0
--- New run! ---
Cost after step 10: 0.5488000. Locality: 1
---Switching Locality---
Cost after step 20: 0.8358000. Locality: 2
Cost after step 30: 0.7614000. Locality: 2
Cost after step 40: 0.6718000. Locality: 2
Cost after step 50: 0.4921000. Locality: 2
---Switching Locality---
---Switching Locality---
Cost after step 60: 0.6433000. Locality: 4
---Switching Locality---
Cost after step 70: 0.7787000. Locality: 5
Cost after step 80: 0.5250000. Locality: 5
---Switching Locality---
Cost after step 90: 0.5270000. Locality: 6
---Switching Locality---
---Switching Locality---
Cost after step 100: 0.9690000. Locality: 8
Cost after step 110: 0.9106000. Locality: 8
Cost after step 120: 0.7561000. Locality: 8
Cost after step 130: 0.4537000. Locality: 8
Cost after step 140: 0.1197000. Locality: 8
Trained: 9
Plateau'd: 0
--- New run! ---
---Switching Locality---
Cost after step 10: 0.6759000. Locality: 2
---Switching Locality---
Cost after step 20: 0.8020000. Locality: 3
Cost after step 30: 0.6412000. Locality: 3
---Switching Locality---
Cost after step 40: 0.6920000. Locality: 4
---Switching Locality---
Cost after step 50: 0.7176000. Locality: 5
Cost after step 60: 0.5973000. Locality: 5
---Switching Locality---
Cost after step 70: 0.5469000. Locality: 6
---Switching Locality---
Cost after step 80: 0.7019000. Locality: 7
Cost after step 90: 0.6006000. Locality: 7
---Switching Locality---
Cost after step 100: 0.8612000. Locality: 8
Cost after step 110: 0.7023000. Locality: 8
Cost after step 120: 0.4108000. Locality: 8
Cost after step 130: 0.1081000. Locality: 8
Trained: 10
Plateau'd: 0
In the global case, anywhere between 70-80% of starting positions are untrainable, a significant number. It is likely that, as the complexity of our ansatz—and the number of qubits—increases, this factor will increase.
We can compare that to our local cost function, where every single area trained, and most even trained in less time. While these examples are simple, this local-vs-global cost behaviour has been shown to extend to more complex problems.
References¶
- 1(1,2)
Cerezo, M., Sone, A., Volkoff, T., Cincio, L., and Coles, P. (2020). Cost-Function-Dependent Barren Plateaus in Shallow Quantum Neural Networks. arXiv:2001.00550